Representación de Datos.
¿Cuál es la diferencia entre datos, información y conocimiento?
- 3 ... es un dato.
- 3 perros ... es un dato.
- 3 perros guardianes ... es un dato.
. 3 perros guardianes cuidando una casa en el verano ...es información.
- 3 perros guardianes cuidando una casa en el verano, implica que no hay moradores ... es conocimiento!!!
Introducción.
Dato: La información se define como los datos que han sido procesados. La información se añade a una representación, la información debe ser oportuna, exacta y compuesta.
Por lo tanto, "dato es la materia prima de cualquier sistema de información y puede ser representativa para algunos, por ejemplo:
Numero35:
- edad de una persona.
- numero favorito.
- numero del departamento de...
- otros significados o totalmente ninguno.
Algunas de las cualidades de la información son: exactitud, oportuna, forma, estructura, etc.
Sistema de Numeración.
Es el conjunto de símbolos utilizados para la representación de cantidades, asi como las reglas que rigen dicha representación.
Un sistema numérico se distingue fundamentalmente por su base, que es el numero de símbolos que utiliza y que, además, se caracteriza por ser el coeficiente que determina cual es el valor de cada símbolo dependiendo de su posición.
Por ejemplo, utiliza como base el 10, que corresponde al numero de símbolos que utiliza para la representación de cantidades. estos símbolos (también denominados dígitos) son:
0,1,2,3,4,5,6,7,8,9
Sistema Binario
Es el sistema numérico que utiliza internamente el hardware, por ello será el sistema mas importante.
Se basa en la representación de cantidades utilizando los dígitos 1 y 0, por tanto su base es 2. Cada digito de un numero representado en este sistema, se denomina BIT (binary digit).
- 4 BIT se denomina cuarteto (1001)
- 8 BIT se denomina octeto o byte (10010110)
- Al conjunto de 1024 bytes, se denomina kilobyte o kb.
- 1024 kb forman un megabyte.
- 1024 megabyte, forman un gigabyte.
Por lo tanto:}
- 1 cuarteto = 4 bits.
- 1 byte = 8 bits.
- 1 kb = 1024*8 bits = 8.192 bits.
- 1 mega= 1024*1024*8= 838.608 bits.
- 1 giga = 1024*1024*1024*8= 8.589.934.592 bits.
Otras bases.
. Base 3: 0,1,2
- Base 5: 0,1,2,3,4
- Base 8: 0,1,2,3,4,5,6,7
- Base 16: 0,1,2,3,4,5,6,7,8,9,A,B,C,D,E,F en donde: A=10, B=11, C=12, D=13, E=14, F=15
Números binarios, decimales y hexadecimales
Decimales
Para entender los números binarios y hexadecimales, lo mejor es entender bien cómo funcionan los números decimales.
Cada dígito de un número decimal va en una "posición", y el punto decimal nos dice qué posición es cada una.
La posición justo a la izquierda del punto son las "unidades". Cada vez que nos movemos a la izquierda vale 10 veces más, y a la derecha vale 10 veces menos:
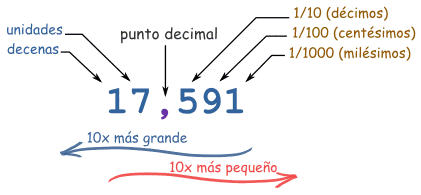
Pero esto sólo es una manera de escribir números. Hay otras maneras como los números romanos, binarios, hexadecimales, y más. ¡Incluso podrías marcar puntos en una hoja de papel!
Contar en diferentes sistemas de numeración
El sistema decimal de numeración también se llama "base 10", porque se basa en el número 10.
En decimal hay diez símbolos (0 a 9), pero fíjate en esto: no hay un símbolo para el "diez". "10" son en realidad dos símbolos juntos, un "1" y un "0":
En decimal contamos 0,1,2,3,4,5,6,7,8,9, entonces decimos "me he quedado sin símbolos, así que empiezo otra vez con 0, pero primero voy a añadir 1 a la izquierda".
En decimal contamos 0,1,2,3,4,5,6,7,8,9, entonces decimos "me he quedado sin símbolos, así que empiezo otra vez con 0, pero primero voy a añadir 1 a la izquierda".
Pero no es obligatorio usar 10 como "base". Podrías usar 2 ("binario"), 16 ("hexadecimal"), ¡o cualquier número que quieras! Sólo sigue la misma regla:
Cuenta hasta justo antes de la "base", después vuelve al 0, pero añadiendo 1 a la izquierda.
Números binarios
Los números binarios son en "base 2" en lugar de "base 10". Empiezas contando 0, después 1, ¡ya se te acabaron los dígitos! Así que vuelves al 0, pero aumentas en 1 el número de la izquierda.
Funciona así:
|
000
|
|
|
001
|
|
|
010
|
no hay "2" en binario, así que volvemos al 0... ... y sumamos 1 a la cifra de la izquierda |
|
011
|
|
|
100
|
volvemos otra vez al 0, y sumamos 1 a la izquierda... ... pero ese número ya es 1 así que vuelve a ser 0... ... y el 1 se suma al siguiente número a la izquierda |
|
101
|
|
|
110
|
etc... |
Números hexadecimales
Los números hexadecimales son interesantes. ¡Hay 16 dígitos diferentes! Son como los decimales hasta el 9, pero después hay letras ("A',"B","C","D","E","F") para los valores de 10 a 15.
Así que con una sola cifra hexadecimal se pueden dar 16 valores diferentes en lugar de los 10 de siempre:
| Decimal: | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Hexadecimal: | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | A | B | C | D | E | F |
Suma de números Binarios.
Tabla de sumar de números binarios
 |
|
|
 |
|
|
Sean los números binarios 00102 y 01102 |
|
|
De la misma forma que hacemos cuando sumamos números del sistema decimal, esta operación matemática la comenzamos a realizar de derecha a izquierda, comenzando por los últimos dígitos de ambos sumandos, como en el siguiente ejemplo: |
 |
|
|
|
|
|
Se suman los siguientes dígitos 1 + 1 = 10 (según la tabla), se escribe el “0” y se acarrea o lleva un “1”. Por tanto, el “0” correspondiente a tercera posición de izquierda a derecha del primer sumando, adquiere ahora el valor “1”. |
Tercer pasoAl haber tomado el “0” de la tercera posición el valor “1”, tendremos que sumar 1 + 1 = 10. De nuevo acarreamos o llevamos un “1”, que tendremos que pasar a la cuarta posición del sumando. |
 |
|
|
|
El valor “1” que toma el dígito “0” de la cuarta posición lo sumamos al dígito “0” del sumando de abajo. De acuerdo con la tabla tenemos que 1+ 0 = 1. |
|
El resultado final de la suma de los dos números binarios será: 1 0 0 0. RESTA BINARIA
Al igual que en la suma, el proceso de resta binaria, se inicia en la columna correspondiente a la de los dígitos menos significativos. |
